Histoire d’eau... chaude

Comment évolue la température de l’eau chaude en fonction du volume consommé la journée quand le chauffe eau ne chauffe que la nuit, c’est à dire en période creuse ? 

Et voilà la bonne question qui m’a fait cogiter pendant des congés.

N’ayant pas trouvé de solution détaillée à cette question je me suis risqué à publier la mienne.

C'était il y a 5 ans, petite mise à jour dans la forme du billet.

Hypothèses de départ

Le problème est traité simplement avec les hypothèses simplificatrices suivantes :

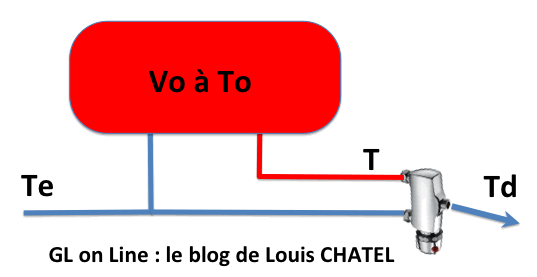
1. la température de l’eau chaude T n’évolue que du fait de la consommation par apport d’eau froide à Te (chauffe eau supposé isolé parfaitement)
2. en début de journée le volume Vo est à la température To
3. l’eau froide et l’eau chaude ont la même chaleur massique et le mélange est supposé instantané à la température d’équilibre entre l’apport en eau froide et le volume restant d’eau chaude.
4. de façon similaire la consommation est faite à une température Td par mélange instantané entre l’eau chaude à la température T et l’eau froide à la température Te… tant que T est supérieur à Td (implicitement de façon initiale To doit aussi être supérieur à Td) et que Te est inférieur à Td bien entendu

Mise en équation et résolution 

Avec ces hypothèses la mise en équation est relativement simple :

Si je consomme dV d’eau chaude il entre dV d’eau froide et la température évolue de telle façon que :  

(T + dT) Vo = T (Vo-dV) +Te dV

Soit 

dT / (T-Te) = - V/Vo

ce qui intégré de To à T donne 

T= Te + (To-Te) exp(-V/Vo) 

ou encore 

exp(-V/Vo) = (T-Te)/(To-Te)

Pour V = 0 on a bien T = To et pour V tendant vers l’infini, T tend vers Te.

V1 correspondant à T = Td est obtenu pour exp(-V1/Vo) = (Td-Te)/(To-Te)

Soit 

V1=Vo Ln((To-Te)/(Td-Te))

Mais jusqu’à cette quantité, l’eau extraite du chauffe eau est toujours d’une température supérieure à Td (pas simple de se doucher dans ces conditions). 

Pour conserver une température constante, pour chaque quantité dV d’eau chaude à T il convient d’injecter une quantité dV* d’eau froide  à Te telle que 

Td (dV+dV*) = T dV + Te dV* soit dV*=dV(T-Td)/(Td-Te)

Où nous remplaçons T par sa fonction de V et obtenons après simplification :

dV*/dV= ((To-Te)/(Td-Te))exp(-V/Vo) -1

Ce qui intégré entre 0 et V1 et en remplaçant exp(-V1/Vo) par son expression en fonction des températures aboutit à l’expression remarquable :

V1 + V1* = Vo (To-Td)/(Td-Te)

Application numérique

Application numérique pour Vo = 100 l, To = 65°, Td = 40° et Te=10° nous avons 

V1= 61 l et V1+V1* = 83 l

Ces résultats obtenus évidemment par excès peuvent s'illustrer de la façon suivante :

Billet mis à jour par Louis CHATEL le 22/02/2022

Pour poursuivre la lecture, les autres billets relatifs aux calculs sont répertoriés dans l'Index de la catégorie "Calcul".