Trains et graphiques : graphique spatial / temporel

Maintenant que nous avons planté le décor, nous pouvons entrer dans le sujet du trajet de notre train en fonction du temps

Construction d'un graphe avec des arrêts 

Maintenant que nous avons un outil pour décrire notre trajet, considérons un trajet avec 2 gares intermédiaires.

Notre train censé circuler à 300km/h s'il ne marque pas d'arrêt mettra une heure pour parcourir les 300km séparant les gares de départ et d'arrivée.

Si notre train marque un arrêt de 4 minutes sa vitesse moyenne va chuter à 281km/h le temps nécessaire à parcourir la distance totale étant allongé d'une phase d'arrêt.

Dans le cas de 2 arrêts là nous tombons à 265km/h (vous pouvez faire les divisions.

Si l'on conclut trop vite à partir de ce graphique on pourrait croire qu'un arrêt du double de temps aura le même impact sur la moyenne, mais ce n'est pas vrai, nous ne pouvons pas écarter les phases d'accélération puis de freinage (dans notre cas 2 arrêts nous avons 3 fois ces 2 phases transitoires à prendre en compte).

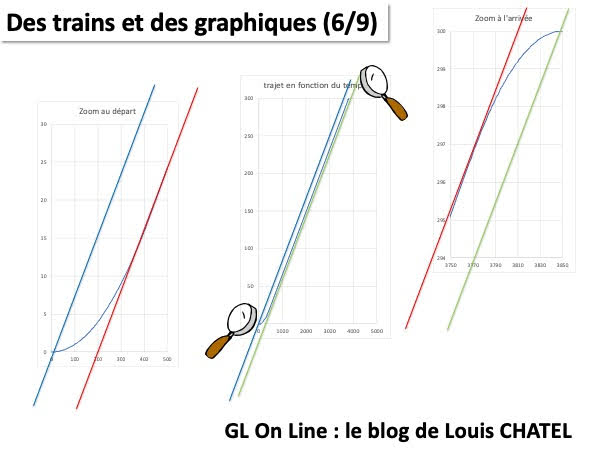
Zoom sur les phases d'accélération et de freinage 

Sur la figure ci-dessus nous avons le "trajet réel" de notre train avec les transitoires d'accélération et de freinage de notre train.

Nous supposons une accélération constante donc faisons apparaître des portions de paraboles comprises entre la portion horizontale (vitesse nulle, tangente à l'axe des abscisses) et la portion tangente à notre droite vitesse constante.

Courbe similaire pour le freinage, à l'échelle près compte tenu d'une accélération différente.

Freinage du train 

Un peu de physique pour fixer les ordres de grandeur. 

Problème qu'on m'avait posé il y a quelques années : 

"sachant qu'un TGV lancé à 300km/h met 3km pour s'arrêter, déterminer le coefficient de frottement roue rail"

Problème de base utilisant les formules de base d'un mouvement uniformément retardé

En notant 

"a" la décélération, 

V la vitesse du train (V=300km/h), 

X la variable de position, variant de X0 à X0+D où D est la distance d'arrêt

t le temps t variant de 0 à T (durée de l'arrêt)

nous avons :

D=X-X0 = 3km = (-a*T^2)/2 + V*T

et V=a*T 

D'où nous pouvons déduire T=V/a et reporté dans l'équation de position nous pouvons déduire notre décélération (en mettant tout dans les bonnes unités bien entendu)

a=V^2 / 2D = 1,17 m/s^2

avec g=9,81 nous avons a/g = 0,11 ce qui correspond au coefficient de frottement pour que ça puisse fonctionner sans glisser (charge répartie sur tous les essieux qui freinent, ce à la limite du glissement).

Nota 1: le temps correspondant est de 71 secondes... alors que pour parcourir la même distance à 300km/h il n'en aurait fallu que 36 (la moitié, propriété remarquable des paraboles quant à l'intersection de la tangente / axe des abscisses).

Nota 2 : pour l'accélération tous les essieux ne sont pas moteurs, la limite de glissement va donc être moindre, pour la suite de la présentation nous prendrons décel = 1 et accel = 0,2 (rapport de masse supposée à 5 entre les motrices et les voitures). 

Ce qui au demeurant représente des niveaux très élevés par rapport au confort des passagers. 

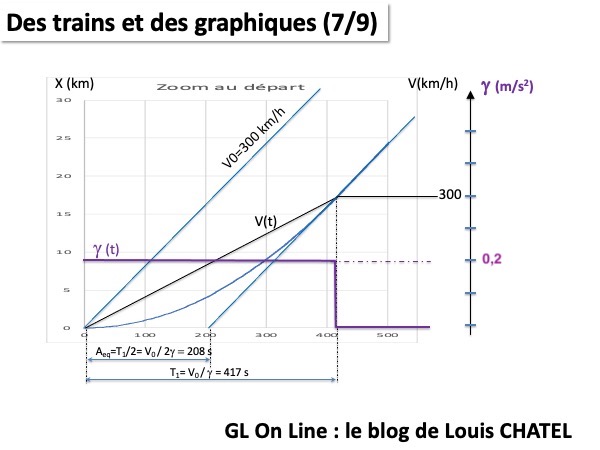
Mise en évidence d'un temps d'arrêt équivalent

Sur la figure ci-dessus nous avons les courbes de position, de vitesse et d'accélération superposées, vitesse et accélération étant à considérer par rapport aux axes de droite.

Comme évoqué plus haut, la tangente à la parabole au point d'atteinte de la vitesse de croisière vient couper l'axe des abscisses à la moitié du temps nécessaire à l'atteinte de cette vitesse de croisière (c'est un bon exercice de démontrer cette propriété).

Avec une accélération de 0,2 m/s^2 on met environ 417s pour atteindre les 300 km/h et tout se passe comme si on avait effectué un arrêt de 208 secondes. 

Si on ajoute la phase d'arrêt à 1m/s^2 il convient d'ajouter un arrêt équivalent de 41s soit un délai supplémentaire d'environ 4 minutes... d'où la chute de la moyenne visualisée.

En conclusion, pour notre exemple avec 2 arrêts il conviendrait d'ajouter 12 minutes (3 fois départ et arrêt) aux 8 minutes d'arrêt effectif soient 20minutes en tout, donc sur 300 km notre TGV roulant normalement à 300 n'aurait qu'une vitesse moyenne de 225km/h

Quand vous lisez des articles sur le journal précisant que les trains roulent moins vite que dans le temps, sur les TER ça s'explique bien si on a ajouté des arrêts. 

En corolaire, un TGV avec plein d'arrêts ce n'est plus vraiment un TGV.

Pour poursuivre la lecture et regarder d'autres applications de ce type de graphique, vous pouvez consulter le billet suivant :  Trains et graphiques : généralisation 

sinon vous pouvez revenir au billet précédent  Trains et graphiques : description du sujet 

ou alors vous pouvez revenir à l'introduction A propos de trains et de graphiques

La vidéo pour ceux qui veulent aller plus vite

Mis à jour Louis CHATEL le 13 juin 2021 

Nota : pour plus de calculs vous pouvez consulter l'Index de la catégorie "Calcul"

Mots clés : trajets, trains, représentation graphique